数据结构
数据结构基本概念
数据结构的基本概念
1.数据:所有能被输入到计算机中,且能被计算机处理的符号的集合。而数据结构中主要讨论结构化
数据。
2.数据元素:是数据(集合)中的一个“个体”,数据结构中的基本单位。表中的一行
3.数据项:一个数据元素可由若数据项组成,数据项是构成数据元素不可分割的单位。表中的一列
4.数据对象:数据对象是具有相同性质的数据元素的集合,是数据的一个子集。一张表或者是这张表的子表
5.关键码:也叫关键字(Key〉,是数据元素中能起标识作用的数据项
6.关系:数据元素之间的关系。数据结构中讨论的元素关系主要是指相邻关系或邻接关系。
7.数据类型是一个值的集合和定义在此集合上一组操作的总称。
(1)原子类型:其值不可再分的数据类型。
(2) 结构类型,其值可以再分解为考干成分(分量)的类型类型。
(3) 抽象数据类型:抽象数据组织和与之相关的操作。
8.数据类型:是一个值的集合和定义在此集合上的一组操作的总称。数据类型和数据结构的关系:数
据类型就是已经实现了的数据结构。
数据结构相关定义
数据结构包括:逻辑结构、存储结构(物理结构)和数据运算(数据操作)
数据的逻辑结构:数据元素之间的逻辑关系(线性和非线性结构)。
存储结构:顺序存储、链式存储、素引存储和散列存储。
数据操作:对数据要进行的运算。运算的定义是针对逻辑结构的,指出运算的功能。运算的实现是针对存储结构的,指出运算的具体操作步骤。
抽象数据类型
ADT 是指一个数学模型以及定义在该模型上的一组操作。
ADT 的定义仅是一组逻辑特性描述,与其在计算机内的表示和实现开关。因此,不论ADT 的内部结构如何变化,只要其数学特性不变,都不影响其外部使用.
ADT 的形式化定义是三元组:ADT=(D,S,P) D其中口是数据对象,S是D上的关系集,P是对D的基本操作集。
ADT Stack { 数据对象: 一个有限线性表 操作集合: push(x) // 将元素x压入栈顶 pop() // 删除并返回栈顶元素 peek() // 返回栈顶元素但不删除 isEmpty() // 判断栈是否为空 size() // 返回栈中元素个数 }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
### 逻辑结构
数据元素之间的关系成为逻辑关系,相应的结构称为逻辑结构
逻辑结构元素决定输入、存储、发送、处理和信息传递的基本操作功能。
逻辑结构的类型:集合:没有关系。线性结构:一对一的关系,树型结构:一对多的关系。图状结构:多对多的关系

### 存储结构
数据结构在计算机内存中的存储包括**数据元素的存储和元素之间的关系的表示**。数据的逻辑结构和物理结构是密不可分的两个方面,一个**算法的设计取决于所选定的逻辑结构**,而**算法的实现依赖于所采用的存储结构**。数据的存储结构有:顺序存储、链式存储、索引存储、散列存储。
1. 顺序存储
1. 用数据元素在存储器中的相对位置来表示数据元素之间的逻辑结构(关系)。
2. 数据元素存放的地址是连续的。
3. 优点是可以实现**随机存取**,每个元素占有最少的存储空间。
4. 只能用相邻的一整块存储单元,可能产生外部碎片
2. 链式存储
1. 每个数据元素增加指针指向另一元素
2. 地址可以不连续
3. 优点:不会出现碎片,充分利用存储单元
4. 缺点:需要额外的指针空间,只能顺序存取
3. 索引存储
1. 建立附加的索引表,格式为(关键字,地址)
2. 优点:检索速度快
3. 缺点:需要额外的索引表空间,增删数据时需要修改索引表
4. 散列存储
1. 散列存储
2. 根据关键字直接计算存储地址(哈希存储)
3. 优点:**检索、增加和删除**操作都很快
4. 可能出现冲突,解决冲突需要额外开销
### 算法
算法定义:是对特定问题求解方法的一种描述,指令的有限序列,每条指令表示一个或多个操作
#### 算法特性
有穷性:算法必须在有限步骤后结束,且每步都在有限时间内完成。
确定性:每条指令必须有明确含义,不存在二义性,**算法只有一个入口和一个出口**。
可行性:算法必须能执行,所有操作都可通过基本运算执行。
输入与输出:输入:可以有零个或多个输入,来自特定对象集合。输出:有一个或多个输出,与输入有特定关系
#### 算法描述
可用多种方法描述:自然语言描述,形式语言描述,计算机程序设计语言描述。
算法和程序的区别:程序是算法用特定程序设计语言的具体实现,**不是所有程序都是算法**。
#### 算法设计的要求
1. 正确性:满足具体问题需求
2. 可读性:易于理解和交流
3. 健壮性:能适当处理非法或错误输入
4. 通用性:处理结果适用于一般数据集合
### 时空复杂度
#### 影响算法效率的因素
- 算法策略选择
- 问题规模
- 程序设计语言
- 编译程序产生的机器代码质量
- 指令执行速度
#### 时间复杂度
常见的时间复杂度(从快到慢):
1. O(1):常量时间阶,执行次数固定
2. O(log n):对数时间阶
3. O(n):线性时间阶
4. O(n log n):线性对数时间阶
5. O(n^k):k≥2,k次方时间阶,执行次数是k次多项式
- 复杂度大小关系:O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(n³)
- 指数与多项式关系:O(2ⁿ) < O(n!) < O(nⁿ)
#### 时间复杂度类型
1. 最坏时间复杂度:最坏情况下的时间复杂度
2. 平均时间复杂度:所有可能输入等概率出现时的期望运行时间
3. 最好时间复杂度:最好情况下算法的时间复杂度
#### 空间复杂度
1. 基本概念:指算法运行所需存储空间的度量,表示为S(n) = O(f(n)),n为问题规模
2. 存储空间包括三个方面:指令常数变量所占空间,输入数据所占空间,辅助存储空间(主要考察这部分)。
1. 常见的空间复杂度:一维数组a[n]:O(n),二维数组a[n][m]:O(n*m),算法原地工作:O(1)
# 线性表

# 树
- 平衡二叉树,或是一棵空树,或符合以下特性:
**【平衡特性1】**:左子树的深度和右子树的深度相差不能超过1,可以是0(代表左右子树深度一样)、-1(代表左子树比右子树少一层)、1(代表左子树比右子树多一层)
**【平衡特性2】它的左右子树也要是平衡二叉树**
查找树,**或是一棵空树**,或满足符合以下特性:
**【查找特性1】**:若左子树不为空,左子树节点**所有的值**均要小于根节点;
**【查找特性2】:** 若右子树不为空,右子树节点**所有的值**均要大于根节点;
**【查找特性3】它的左右子树也要是查找树**
如果是**二叉树**,那么必须要**先序+中序**,或者**中序+后序**,但是题目中说的是**树**,**树的先序(根)== 二叉树的先序**,**树的后序(根)== 二叉树的中序**,所以是一定**可以构造出来**的。
# 图

一个图G 若满足:①不存在重复边;②不存在顶点到自身的边,则称图G为**简单图**。
若图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联,则G为**多重图**。
**完全图**:任意两个顶点之间都存在边
**连通、连通图和连通分量**
在无向图中,若**从顶点v到顶点w 有路径存在**,则称v 和w 是**连通**的。**若图G 中任意两个顶点都是连通的**,则称图G为**连通图**,否则称为非连通图。**无向图中的极大连通子图称为连通分量**。若一个图有n个顶点,并且边数小于n − 1,则此图必是非连通图。如下图(a)所示,
有3个连通分量

在有向图中,若从顶点v 到顶点w 和从顶点w 到项点v 之间**都有路径,**则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的,则称此图为强连通图。**有向图中的极大强连通子图**称为有向图的强连通分量
图的深度类似于数的先序遍历,图的广度类似于树的层次遍历
无向图: vi的度=所连边数=矩阵第i行(或者i列)中1的个数。 有向图: vi的度数=入度+出度=第i行元素之和+第i列元素之和(这里元素指1)
要保证在任意连接方式下都能连通具有10个顶点的无向图,至少需要()条边
(n-2)%7D%7B2%7D%2B1)
第一个顶点和最后一个顶点相同的路径称为**回路**;序列中顶点不重复出现的路径称为**简单路径**;回路显然不是**简单路径**
存在回路的有向图不存在拓扑序列,若**拓扑排序输出结束**后所**余下的顶点都有前驱**,则说明只得到了部分顶点的拓扑有序序列,图中存在回路

如上图的AOE网,在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;网中也仅存在一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。我们把路径上各个活动所持续的时间之和称为路径长度,**从源点到汇点具有最大长度的路径叫关键路径,在关键路径上的活动叫关键活动。**
**完成整个工程的最短时间就是关键路径的长**度,即**关键路径上各活动花费开销的总和**。这是因为关键活动影响了整个工程的时间,即若关键活动不能按时完成,则整个工程的完成时间就会延长。因此,只要找到了关键活动,就找到了关键路径,也就可以得出最短完成时间。
对于关键路径,需要注意以下几点:
①关键路径上的所有活动都是关键活动,它是决定整个工程的关键因素,因此可通过加快关键活动来缩短整个工程的工期。但也不能任意缩短关键活动,因为一旦缩短到一定的程度,该关键活动就可能会变成非关键活动。
②网中的关键路径并不唯一,
且对于有几条关键路径的网,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
**判断有向图是否存在环**的2种方法(深度遍历,拓扑排序)
带权的连通无向图的**最小代价生成树**不唯一的,只有当权值不相同时才唯一,**最小代价唯一**,树不唯一,因为可能有的边权值相同,导致有多种组成方式的树

在n个结点的无向图中,若该图是连通图,则其边数大于等于n-1,
在n个结点的无向图中,若边数大于(n-2)(n-1)/2,则该图必是连通图

6个城市,顶多4个中间城市,因为先经过A再经过B和先经过B再经过A是不一样的,所以用排列数
途径0个中间城市: A(0,4) = 1
途径1个中间城市: A(1,4) = 4
途径2个中间城市: A(2,4) = 12
途径3个中间城市: A(3,4) = 24
途径4个中间城市: A(4,4) = 24
拓扑有序序列: 把AOV网络中各顶点按照他们相互之间的优先关系排列到一个线性序列的过程。若vi 是vj前驱,则vi 一定在vj,对于没有优先关系的点, 顺序任意。
AOV网 (Activity On Vertex Network)
- 用顶点表示活动,用弧表示活动之间的优先关系
- 是一个有向无环图(DAG)
- 若从顶点i到顶点j有一条弧,表示活动i必须在活动j之前完成
- 常用于表示工程项目中各个活动之间的先后顺序
- 主要用于确定活动的执行次序,比如课程的先修关系
AOE网 (Activity On Edge Network)
- 用边表示活动,用顶点表示事件
- 也是一个有向无环图(DAG)
- 边上的权值表示完成该活动所需的时间
- 顶点表示某些活动完成的事件节点
- 从源点到汇点具有最大路径长度的路径叫做关键路径
- 主要用于工程估算,可以:
- 计算整个工程完成的最短时间
- 找出关键路径
- 确定哪些活动是关键活动

必须完成1-6所有的关键路径上的关键活动,才算完成工程
这个网有三条关键路径: 1. b、d、c、g 2. b、d、e、h 3. b、f、h 缩短工期的活动要涵盖三条路径。
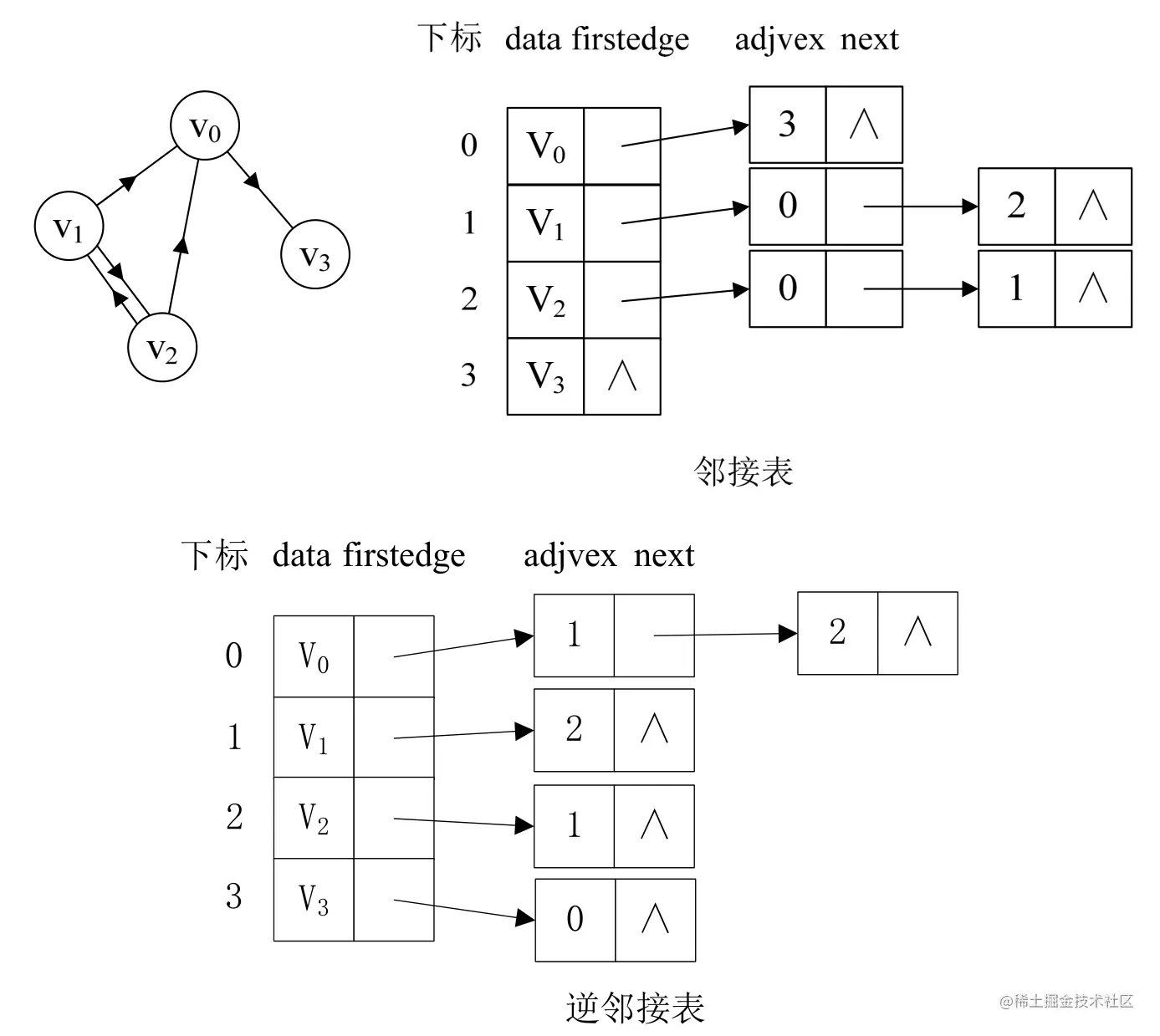
无向图:多重链接表
有向图:十字链表&边集数组
共有:邻接表&邻接矩阵
从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径。把关键路径上的活动称为关键活动
完成整个工程的最短时间就是关键路径的长度,也就是关键路径上各活动花费开销的总和。这是因为关键活动影响了整个工程的时间,即如果关键活动不能按时完成的话,整个工程的完成时间就会延长。因此,只要找到了关键活动,就找到了关键路径,也就可以得出最短完成时间。
在一个有向图的拓扑序列中,若顶点 a 在顶点 b 之前,则图中必有一条a到b的路径
Bellman-Ford 算法 这是一个解决带负权边的单源最短路径问题的算法。
主要特点:
1. 可以处理负权边,能检测负权回路
2. 时间复杂度 O(VE),其中 V 是顶点数,E 是边数
3. 基本思想:对所有边进行 V-1 次松弛操作
Kruskal 算法 这是一个构建最小生成树的贪心算法。适合边少的情况
主要特点:
1. 时间复杂度 O(E log E),主要来自边的排序
2. 使用并查集数据结构判断是否形成环
3. 适合稀疏图
Prim 算法 另一个构建最小生成树的贪心算法。适合顶点少的情况
主要特点:
1. 时间复杂度 O(E log V)(使用二叉堆实现)
2. 从单个顶点开始逐步扩展
3. 适合稀疏图
Dijkstra 算法 解决非负权边的单源最短路径问题。

Dijkstra是一种用来求单源最短路径的算法。
**单源是**什么意思?
从一个顶点出发,Dijkstra算法只能求一个顶点到其他点的最短距离而不能任意两点。
**算法思想**:
维护一个集合 S,集合内的点是已经确定最短路径的结点;
每次操作找出与集合相邻的点中距离起点最近的结点加入集合中,并确定它的最短路径值为它的前一已确定结点的最短路径值+该边权值,存在dis数组中。
**算法流程**:
首先把结点1加入集合(红色结点),蓝色结点为相邻结点, s={1},dis[]={0,∞,∞,∞,∞,∞,∞,∞}
与S相邻的结点为2、3、5,把相邻结点路径最短的加入集合(即结点5) s={1,5},dis[]={0,1,∞,∞,∞,∞,∞,∞}
与S相邻的结点为2、3、6、8,把相邻结点路径最短的加入集合(即结点3) s={1,5,3},dis[]={0,1,2,∞,∞,∞,∞,∞}
与S相邻的结点为2、4、6、8,把相邻结点路径最短的加入集合(即结点2和4) s={1,5,3,2,4},dis[]={0,1,2,3,3,∞,∞,∞}
与S相邻的结点为6、7、8,把相邻结点路径最短的加入集合(即结点8) s={1,5,3,2,4,8},dis[]={0,1,2,3,3,4,∞,∞}
与S相邻的结点为6、7,把相邻结点路径最短的加入集合(即结点6和7) s={1,5,3,2,4,8,6,7},dis[]={0,1,2,3,3,4,5,5}
# 排序
插入排序平均时间复杂度为O(n^2) 插入排序最坏情况时间复杂度为O(n^2)
冒泡排序平均时间复杂度为O(n^2) 冒泡排序最坏情况时间复杂度为O(n^2)
堆排序平均时间复杂度为O(nlogn)
希尔排序平均时间复杂度大致为O(n^1.5)
归并排序平均时间复杂度为O(nlogn) 归并排序最坏情况时间复杂度为O(nlogn)
快速排序最坏情况时间复杂度为O(n^2)
数组元素,基本有序,所以快速排序是最慢的,因为会退化成冒泡排序 选择排序时间复杂度都是O(n^2),堆排序都是O(nlogn),但是基本有序对插入排序是最好的 因为这样只需要比较大小,不需要移动,时间复杂度趋近于O(n)
不稳定的含义是建立在有两个相同元素在排序前后,相对位置发生了变化。
### 基数排序
基数排序是通过“分配”和“收集”过程来实现排序。
1)首先根据个位数值(只看个位)来排序:
253 674 924 345 627
2)再看十位(只看十位数值大小)来排序:
924 627 345 253 674
3)最后看百位:
253 345 627 674 924

**快速排序的原理**:**通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都不大于基准值,另一部分不小于基准值,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归****进行,以此达到整个数据变成有序序列。**最差情况下时间复杂度** :最差的情况就是每一次取到的元素就是数组中最小/最大的,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序) 这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n2+ n; 综上所述:快速排序最差的情况下时间复杂度为:O( n2 ),快速排序的最坏情况基于每次划分对基准值的选择,基本的快速排序选取第一个元素作为基准。这样在**数组已经有序的情况下,每次划分将得到最坏的结果**。
直接选择排序的时间复杂度与初始排序无关(关键字比较次数与记录的初始排列无关的)
已知数据表A中每个元素距其最终位置不远,为节省时间排序,应采用直接插入排序
堆排序的时间复杂度是O(n*log(n)),堆排序中建堆过程的时间复杂度是O(n)
建堆有2种方法
第一种方法:**HeapInsert**(本题就是这种方法),它可以假定我们事先不知道有多少个元素,通过不断往堆里面插入元素进行调整来构建堆。这种插入建堆的时间复杂度是**O(NlogN)**
第二种方法:**Heapify**
从最后一个非叶子节点一直到根结点进行堆化的调整。如果当前节点小于某个自己的孩子节点(大根堆中),那么当前节点和这个孩子交换。这种建堆的时间复杂度是**O(N)**
Heapify是一种类似下沉的操作,HeapInsert是一种类似上浮的操作。
待排序元素规模较小时,宜选取哪种排序算法效率最高冒泡排序
在最好情况下,下列排序算法中 排序算法时间复杂度最低的是直接插入排序。
希尔排序的思想是:先将待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成),分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。